


加拿大安省12年级微积分与向量(Calculus and Vectors)课程是建立在学生以前的函数经验和他们对变化率的理解的基础上。本课程主要解决三维空间中矢量的几何和代数表示以及直线和平面表示的问题,拓宽对变化率的理解,包括多项式、正弦、指数、有理和根式函数的导数;并将这些概念和技能应用到现实世界关系的建模中。本课程面向选择在科学、工程、经济和一些商业领域从事职业的学生,包括那些需要学习大学水平的微积分、线性代数或物理课程的学生。
OSSD课程介绍
加拿大安省12年级微积分与向量(Calculus and Vectors)课程是建立在学生以前的函数经验和他们对变化率的理解的基础上。本课程主要解决三维空间中矢量的几何和代数表示以及直线和平面表示的问题,拓宽对变化率的理解,包括多项式、正弦、指数、有理和根式函数的导数;并将这些概念和技能应用到现实世界关系的建模中。本课程面向选择在科学、工程、经济和一些商业领域从事职业的学生,包括那些需要学习大学水平的微积分、线性代数或物理课程的学生。
1/微积分导论 |
本单元主要理解基本的微积分概念,然后处理变化率问题和极限概念,并使用这个概念的几个例子,延伸和扩展到能够区分平均变化率和瞬时变化率,以帮助学生解决现实应用中出现的问题。 |
2/导数 |
导数的概念本质上是一种确定切线斜率函数的捷径,通常需要极限的概念。一旦从极限的评估中看到模式,就可以建立规则来简化确定这个斜率函数所必须做的事情。本单元首先研究这些规则,包括:幂规则、乘积规则、商规则和链式规则,然后研究复合函数的导数。 |
3/指数、对数和三角函数的导数 |
在这一单元,将主要学习指数和对数的变化率,涵盖指数函数的导数及其应用。本单元也将学习对数和三角函数的导数。 |
4/曲线图形 |
本单元主要使用一阶导数测试确定多项式函数图形的最大值和最小值;使用二阶导数测试来确定凹度区间;根据给定的方程,用5个步骤画出多项式函数的图形。本单元将帮助学生理解使用微积分帮助我们绘制曲线的基本原理,并解决一些基本的优化问题。 |
5/微分的应用和相关利率 |
本单元将学习如何计算隐式微分和对数微分,应用导数概念绘制速度-时间和加速度-时间图,解决现实世界应用中出现的问题,如人口和人口变化率、流量和流速、高度和增长率。 |
6/向量介绍 |
在本单元,将学习如何定义一个向量,它是一个既有大小又有方向的量,本单元还学习区分标量和矢量,学习图形和代数上的加、减向量,使用角度系统、方向系统和方位系统表示二维空间中的向量,并解决涉及二维向量运算的现实世界问题。 |
7/向量应用 |
本单元主要涉及功和扭矩的应用用于引入笛卡尔向量的点积和叉积,笛卡尔矢量的矢量投影和标量投影是用点积来表示的。本单元还需要研究并证明了向量乘积的性质,讨论矢量积,以预测线与面的交点中的线与面的系统的解的特征。 |
8/三维空间中的线条 |
本单元中存在各种类型的问题,通常分为以下几类:勾股定理问题(包括阶梯和交叉问题)、体积问题(通常涉及填充或清空三维形状)、波谷问题、阴影问题和一般速率问题。在这一单元中,将分别研究这些类型的问题。 |
9/平面 |
在这一单元,将从几何和代数的角度认识平面的法线,确定两个平面重合或者是两个不同的平行平面的情况,并确定与另外两个平面相交于一点或多点的平面方程。 |
10/矩阵和线性系统 |
本单元主要学习将线性系统转化为矩阵;加、减、乘矩阵,用矩阵运算确定三个平面的交点。 |
1/微积分导论
本单元主要理解基本的微积分概念,然后处理变化率问题和极限概念,并使用这个概念的几个例子,延伸和扩展到能够区分平均变化率和瞬时变化率,以帮助学生解决现实应用中出现的问题。
2/导数
导数的概念本质上是一种确定切线斜率函数的捷径,通常需要极限的概念。一旦从极限的评估中看到模式,就可以建立规则来简化确定这个斜率函数所必须做的事情。本单元首先研究这些规则,包括:幂规则、乘积规则、商规则和链式规则,然后研究复合函数的导数。
3/指数、对数和三角函数的导数
在这一单元,将主要学习指数和对数的变化率,涵盖指数函数的导数及其应用。本单元也将学习对数和三角函数的导数。
4/曲线图形
本单元主要使用一阶导数测试确定多项式函数图形的最大值和最小值;使用二阶导数测试来确定凹度区间;根据给定的方程,用5个步骤画出多项式函数的图形。本单元将帮助学生理解使用微积分帮助我们绘制曲线的基本原理,并解决一些基本的优化问题。
5/微分的应用和相关利率
本单元将学习如何计算隐式微分和对数微分,应用导数概念绘制速度-时间和加速度-时间图,解决现实世界应用中出现的问题,如人口和人口变化率、流量和流速、高度和增长率。
6/向量介绍
在本单元,将学习如何定义一个向量,它是一个既有大小又有方向的量,本单元还学习区分标量和矢量,学习图形和代数上的加、减向量,使用角度系统、方向系统和方位系统表示二维空间中的向量,并解决涉及二维向量运算的现实世界问题。
7/向量应用
本单元主要涉及功和扭矩的应用用于引入笛卡尔向量的点积和叉积,笛卡尔矢量的矢量投影和标量投影是用点积来表示的。本单元还需要研究并证明了向量乘积的性质,讨论矢量积,以预测线与面的交点中的线与面的系统的解的特征。
8/三维空间中的线条
本单元中存在各种类型的问题,通常分为以下几类:勾股定理问题(包括阶梯和交叉问题)、体积问题(通常涉及填充或清空三维形状)、波谷问题、阴影问题和一般速率问题。在这一单元中,将分别研究这些类型的问题。
9/平面
在这一单元,将从几何和代数的角度认识平面的法线,确定两个平面重合或者是两个不同的平行平面的情况,并确定与另外两个平面相交于一点或多点的平面方程。
10/矩阵和线性系统
本单元主要学习将线性系统转化为矩阵;加、减、乘矩阵,用矩阵运算确定三个平面的交点。
同步辅导
了解学生的基础和能力,以MCV4U大纲为基础,全面讲解知识点,系统学习知识模块,了解课程考试的重点和难点,熟悉历次考试的题型和模块。
因材施教
因材施教,为学生量身定做学习计划,帮助学生提高成绩,根据学生的学习特点,有针对性地整理难点,使学生对课程考试内容有清晰的了解。
经验丰富
多年的加拿大课程辅导经验,拥有MCV4U课程题库、原版教材及真题资料,帮助学生做相应的练习,让学生更好地理解和消化学习内容。
教学完善
采用在线一对一形式,中文或英文双语进行授课,拥有专业完善的教育教学体系,帮助学生全面构建自己的知识框架。
答:OSSD课程是加拿大安大略省中学文凭,也是非常有优势的一个国际课程体系,OSSD课程科目种类非常丰富,尤其是12年级的课程,12年级的课程成绩也是申请大学的成绩,对学生们来讲尤其重要。 MCV4U是OSSD课程的重要的科目,也
答:MCV4U课程是加拿大安省OSSD课程12年级课程,课程全称为Calculus And Vectors微积分与向量。惟世国际教育提供加拿大MCV4U辅导课程,17年教学经验,真人名师一对一在线实时授课,有需要帮忙提升成绩的同学可以直接在
答:MCV4U课程是加拿大安省高中12年级的微积分与向量(Calculus and Vectors)课程,这门课程是建立在学生以前的函数经验和他们对变化率的理解的基础上的。相信很多学生对于这门课程还不是很了解,下面考而思惟世为大家介绍一下。
MCV4U最新资讯
最新MCV4U报考资讯 掌握最新动态

MCV4U是微积分向量(CalculusandVectors)课程,是加拿大安省12年级非常重要的一门科目,近期来惟世国际教育辅导这门课程的学生也比较多。下面为大家介绍一下我们的加拿大12年级微积分向量MCV4U在线课程。 MCV
 2025-11-05 15:31:03
2025-11-05 15:31:03
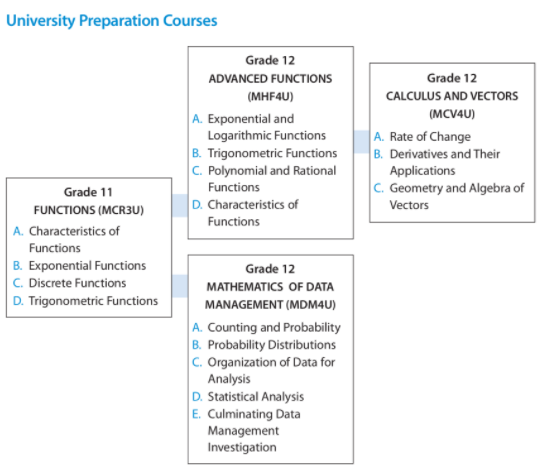
加拿大安省12年级OSSD数学课程包括MHF4U(高等函数)、MCV4U(微积分与向量)、MDM4U(数据管理数学)三门,这三门均为12年级University Preparation课程,都是OSSD课程非常重要的科目,下面我们来具体
 2025-10-13 12:41:48
2025-10-13 12:41:48

在国际课程中,MCV4U课程是高中数学的重要组成部分,许多学生在学习过程中遇到了各种挑战。随着教学要求越来越高,许多学生开始寻求有效的辅导方式,以便更好地掌握知识点和提升成绩。今天,我们将探讨MCV4U课程的学习方法,帮助你找到合适的辅
 2025-04-29 14:20:06
2025-04-29 14:20:06

OSSD课程是加拿大安省的高中课程,在OSSD课程中,微积分也是非常重要的科目,加拿大12年级OSSD微积分课程代码为MCV4U,今天考而思惟世为大家详细介绍一下MCV4U课程,感兴趣的小伙伴可以来了解一下哦~
 2025-02-18 14:16:53
2025-02-18 14:16:53

考而思惟世提供加拿大OSSD数学辅导,包括MHF4U(高等函数)、MCV4U(微积分与向量)、MDM4U(数据管理数学),采用在线一对一个性化辅导,老师均可中英双语授课,有需要的小伙伴可以直接在线咨询哦。 MHF4U课程
 2025-01-30 10:23:20
2025-01-30 10:23:20

OSSD课程是加拿大安省的高中课程,在OSSD课程中,微积分也是非常重要的科目,加拿大12年级OSSD微积分课程代码为MCV4U,今天考而思惟世为大家详细介绍一下MCV4U课程,感兴趣的小伙伴可以来了解一下哦~
 2025-01-07 11:43:08
2025-01-07 11:43:08

OSSD课程是加拿大安大略省中学文凭,也是非常有优势的一个国际课程体系,OSSD课程科目种类非常丰富,尤其是12年级的课程,12年级的课程成绩也是申请大学的成绩,对学生们来讲尤其重要。 MCV4U是OSSD课程的重要的科目,也
 2026-01-16 16:56:30
2026-01-16 16:56:30

MCV4U课程是加拿大安省OSSD课程12年级课程,课程全称为Calculus And Vectors微积分与向量。惟世国际教育提供加拿大MCV4U辅导课程,17年教学经验,真人名师一对一在线实时授课,有需要帮忙提升成绩的同学可以直接在
 2025-08-22 12:31:54
2025-08-22 12:31:54

MCV4U课程是加拿大安省高中12年级的微积分与向量(Calculus and Vectors)课程,这门课程是建立在学生以前的函数经验和他们对变化率的理解的基础上的。相信很多学生对于这门课程还不是很了解,下面考而思惟世为大家介绍一下。
 2025-06-03 15:45:36
2025-06-03 15:45:36

咨询电话
客服电话: 132-6331-8174
免费电话咨询服务,放心接听!

在线咨询

微信客服

客服微信:KesWish

回到顶部