A-Level进阶数学FP1& FP12学习指南！

CAIE考试局A-Level进阶数学(9231)，是中国学生特别爱选的科目之一。进阶数学是A-Level基础数学(9709)课程的扩展与延伸，其学习内容相较于基础数学更加深入和广泛，涵盖了更多的纯数、力学和统计学知识。在学习进阶数学（9231）之前，学生通常已完成或正在学习A-Level数学（9709）。

A-Level进阶数学学什么？

CAIE A-Level进阶数学共4个知识模块，对应考察4个paper，各模块均为必选。

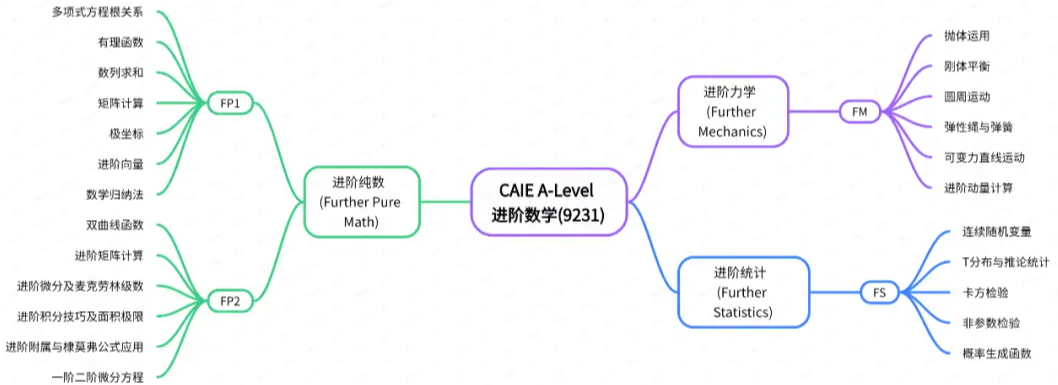
1、进阶纯数FP1 (FurtherPure Math)：知识点包含多项式方程的根、有理函数及其图像、数列求和、矩阵计算、极坐标、进阶向量、数学归纳法。

2、进阶纯数FP2 (FurtherPure Math) ：双曲线函数、进阶矩阵计算、进阶微分、进阶积分、进阶复数、一阶二阶微分方程。

3、进阶力学FM (Further Mechanics) ：抛体运动、刚体平衡、圆周运动、胡克定律、变力作用下的直线运动、进阶动量计算。

4、进阶统计FS (Further Statistics) ：连续随机变量、T分布与推论统计、卡方检验、非参数检验、概率生成函数

进阶数学 4个模块的考试为有限组合：

组合1：AS选修FP1+FS，A2选修FP2+FM

组合2：AS选修FP1+FM，A2选修FP2+FS

2026年进阶数学新考纲

进阶数学难不难？哪些学生适合选？

进阶数学的A*率相对较高，但并不意味着它容易拿高分，因为学习内容相对复杂和抽象，对学生的抽象思维、逻辑推理和数学证明能力提出更高要求。所以更适合对数学有浓厚兴趣、数学基础扎实，GCSE和AS阶段数学基础扎实、成绩优异（如数学9分A*）的学生。

基于未来专业需求，比如许多顶尖大学的专业特别是与数学、物理、工程等相关的专业，会要求或优先考虑学生提交A-Level进阶数学的成绩，招生时也都会明确列出对A-Level进阶数学的要求，学生需要根据自己的专业方向选择是否学习进阶数学。

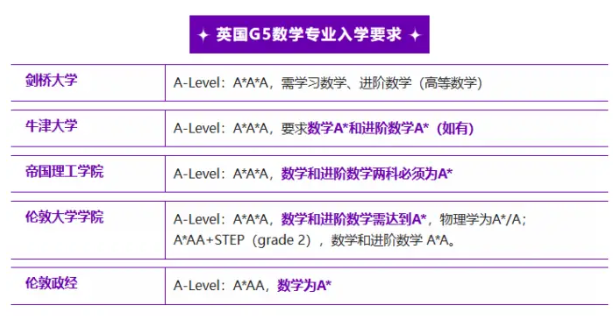
如果是申请牛剑G5等顶级学校数学、物理、工程、经济等对数学能力要求较高的专业，优秀的A-Level进阶数学的成绩，将起到重要的加分作用，常见选课组合是：【进阶数学+数学+物理】。

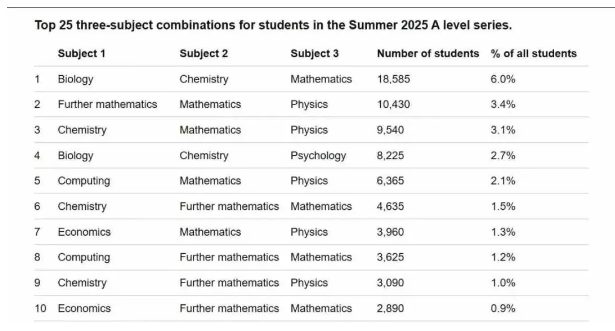
A-Level十大最受欢迎选课组合：

生物+化学+数学，占总人数的6%

进阶数学+数学+物理，占比3.4%

化学+数学+物理居第三，为3.1%

如何学好A-Level进阶数学？

熟悉教材和考试大纲是掌握一门学科的基础。在学习过程中，建议根据自己的学习进度和理解能力，逐步构建知识体系，同时，留出足够的时间进行知识点的整合和复习回顾，确保对所学内容有全面而深入的理解。

今天这篇【进阶纯数全攻略】，我们就带各位小伙伴们来深度解析CAIE A-Level 进阶数学9231考纲，带你系统梳理纯数模块的具体知识点。

进阶纯数FP1&FP2的区别和联系

进阶纯数1（FP1）的大部分内容相对独立于A-Level基础数学的P3，但要求学生已经掌握基础数学P1和P3的核心技能（如代数、微积分、复数基础）。

进阶纯数2（FP2）则依赖FP1的知识基础，并将数学工具推向更高阶、更综合的应用。例如，FP2的双曲函数、矩阵对角化、高阶微分方程，都建立在FP1的代数、矩阵和微积分基础之上。

FP1 偏重知识扩展与维度提升：从实数到复数，从二维向量到三维向量，从多项式到有理函数，从直角坐标到极坐标，它拓宽了数学的知识疆界。

FP2 偏重理论深化与综合建模：将已有的工具（如矩阵、微积分）用于解决更复杂的理论问题（特征值、级数、微分方程），并引入全新的函数体系（双曲函数）和强大的理论工具（棣莫弗定理）。

进阶数学纯数1&2知识点梳理

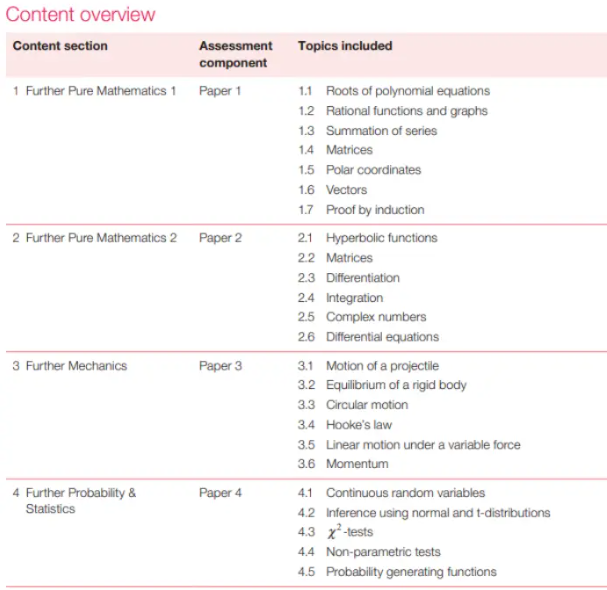
模块1：进阶纯数1（Paper 1）

Further Pure Mathematics 1

进阶数学的第一道门槛，AS和 A-level必修模块。

考试时长：2小时

题型：6-8道结构化大题，全部必答

分值：75分（AS占60%，A Level占30%）

这个模块内容覆盖多项式方程的根、有理函数及其图像、数列求和、矩阵计算、极坐标、进阶向量、数学归纳法等多个维度，矩阵部分是重难点。

1.1 Roots of Polynomial Equations多项式方程的根

核心内容：根与系数的关系（韦达定理的扩展）。

重难点：对称函数求值，通过变量替换构造新方程，尤其是当新根与旧根存在非线性关系时。

高频考点：结合未知系数，利用根与系数的关系建立方程求解。常考对称函数求值、未知系数确定，一般只涉及2、3、4次方程。代换过程需要逆向思维。题目不会给出最直接的代换（如平方、倒数），而是更隐蔽的关系。学生必须理解代换的本质是建立新旧根的联系。

1.2 Rational Functions & Graphs有理函数与图像

核心内容：绘制有理函数图像，掌握垂直渐近线（分母为零的点）、水平渐近线（比较分子分母最高次项）、斜渐近线（当分子次数比分母高一次时，用多项式除法得到）、与坐标轴的交点、极值点（可能需要导数或判别式判断）。理解函数图像的变换（如 y = f(x) 与 y = |f(x)|、y = f(|x|) 的关系）

重难点：准确画出斜渐近线，并理解函数在无穷远处的行为，判断函数的值域（通过判别式法或其他方法）。

高频考点：图像特征（极值点、渐近线、交点）必须清晰标注，常结合方程与不等式出题，一些同学经常会混淆不同变换的规则导致丢分。

1.3 Summation of Series数列求和

核心内容：标准求和公式的应用与推广，熟练运用Σr、Σr²、Σr³ 公式并解决相关变体。

差分法，这是本模块的核心技巧。

收敛性与无穷级数，通过观察部分和Sn的表达式，当 n→∞时，判断级数是否收敛，并求其和。

重难点：Σr、Σr²、Σr³ 的推广使用，差分法求有限级数和。

高频考点：使用部分分式化简通项，并判断级数收敛性。使用差分法求有限项和，题目常与代数、三角函数结合。

1.4. Matrices矩阵

核心内容：基本运算（加、减、乘法，零矩阵，单位矩阵I）；行列式与逆矩阵，几何变换，不变点与不变线。

重难点：矩阵运算、逆矩阵、行列式、几何变换。理解矩阵表示几何变换（旋转、反射、伸缩、剪切），求解不变线，特别是那些不通过原点的不变线。

高频考点：给出一个几何图形和其变换后的图形，求变换矩阵；计算组合变换的矩阵；求变换的面积比例因子或描述变换效果。尤其关注不变点与不变线。

1.5 Polar Coordinates极坐标

核心内容：坐标转换；极坐标曲线绘制，需关注对称性（关于初线、极点）、在极点处的行为（r=0 时）、r 的最大最小值、与初线的交点；扇形面积公式。

重难点：难点在于绘制形状复杂的曲线，将直角坐标方程转化为简洁的极坐标方程、绘制极坐标曲线；利用公式求扇形面积。

高频考点：计算由两条极坐标曲线所围区域的面积。求曲线的切线或特定点的坐标，图像注意体现对称性、与极轴交点、极值点。

1.6 Vectors进阶向量

核心内容：平面方程三种形式转换、向量叉积、几何应用（综合难点）；求线与面交点、点到平面垂足、两平面交线、异面直线最短距离。

重难点：求解异面直线问题。几何想象与代数计算的结合。理解向量积结果的几何意义。异面直线的公垂线和最短距离是经典难题。

高频考点：向量法是解决空间几何问题的利器，计算量可能较大。求线面交点、点到平面距离、两平面夹角。利用向量积求平面的法向量或三角形的面积。

1.7 Proof by Induction数学归纳法

核心内容：标准三步法，奠基（n=1成立）、归纳假设（假设n=k成立）、归纳递推（证明n=k+1成立）。

应用类型：证明求和公式、数列通项公式、矩阵幂等式、整除性问题。

猜想与证明：先通过观察n=1,2,3的情况猜想结论，再用归纳法证明。

重难点：用归纳法证明等式、整除性、矩阵幂等，在递推步骤中，如何巧妙地利用归纳假设进行代数变形；从有限试验中猜想通项并证明。

考点提示：常与数列、矩阵、整除问题结合。

模块2：进阶纯数2（Paper 2）

Further Pure Mathematics 2

在进阶纯数1的基础上，进阶纯数2更深入、更抽象，A-Level必修模块。

时长：2小时

题型：7-9道结构化大题，全部必答

分值：75分（A-Level占30%）

特点：深度和广度都超过Paper 1，强调综合应用

FP2的内容包含双曲线函数、进阶矩阵计算、进阶微分、进阶积分、进阶复数、一阶二阶微分方程，尤其是双曲函数、复数与微分方程部分学起来有点难度。

2.1 Hyperbolic Functions双曲线函数

核心内容：理解双曲线函数定义并绘制图像，掌握其图像特征（奇偶性、单调性、渐近线）；证明并使用双曲线函数的恒等式；反双曲线函数及其对数形式（重点），必须会推导和熟练使用

重难点：记忆和理解与三角函数的异同，与三角函数类比但不等同，需注意符号与性质差异。反函数对数形式的推导（解二次方程并选择符号）。

高频考点：解双曲线函数方程、恒等式证明、反函数的求导与积分是常见题型。

2.2 Matrices进阶矩阵

核心内容：线性方程组与矩阵，将三元一次方程组表示为矩阵方程 Ax=b。理解解的三种情况（唯一解、无穷多解、无解）与矩阵行列式（是否奇异）的关联，并能几何解释（三个平面相交于一点、一线或没有公共点）。

特征值与特征向量（重点）：

定义：对于方阵A，若存在数λ和非零向量v使得 Av=λv，则λ是特征值，v是对应特征向量。

求解：解特征方程 det(A−λI)=0 得特征值，代入 (A−λI)v=0求特征向量。

矩阵对角化，以及凯莱-哈密顿定理（矩阵满足其自身的特征方程）。

重难点：线性方程组解的讨论，理解方程组解与矩阵奇异性的几何意义（平面交线、交点），理解特征值和特征向量的几何意义（变换下方向不变的轴向和缩放因子），处理重特征值或复数特征值的情况（考纲通常要求实特征值），完成对角化的全过程。

高频考点：2×2与3×3矩阵特征问题常考，对角化用于求矩阵幂，利用凯莱-哈密顿定理简化矩阵多项式计算。

2.3 Differentiation进阶微分

核心内容：双曲函数与反三角函数的导数、隐函数与参数方程二阶导；麦克劳林展开推导（尤其是前几项），不包括一般项的推导，但可能需要连续的“隐式”求导步骤。

重难点：积分递推公式，通过分部积分或巧妙构造递推关系。

高频考点：常与后续的积分、级数问题结合出题。

2.4 Integration进阶积分

核心内容：双曲函数积分、三角/双曲代换、递推公式、弧长与旋转体表面积；递推公式构造与证明，矩形法逼近面积。

高频考点：积分技巧要求高，常涉及换元、分部积分等复合运用。

2.5. Complex Numbers进阶复数

核心内容：理解和证明棣莫弗定理，三角函数幂与倍角关系，n次单位根，用复数方法求三角级数和（C + iS 方法）。

重难点：棣莫弗定理与三角变换，复数求和要灵活运用 C + iS 方法化简三角级数。

高频考点：复数与三角恒等变换结合是经典难题，需灵活转换视角。

2.6. Differential Equations微分方程

核心内容：一阶线性微分方程（积分因子法）和二阶常系数线性微分方程（重点），包括齐次方程、非齐次方程，理解和进行变量替换。

重难点：二阶常系数线性微分方程；正确选择特解形式，尤其是当 f(x)的形式与CF部分重复时（“共振”情况），变量替换简化方程。

高频考点：一阶与二阶微分方程求解，二阶常系数线性微分方程（包括求CF和PI），熟练掌握齐次解与特解的组合，理解微分方程在实际建模中的应用（如弹簧振动、电路）。